
















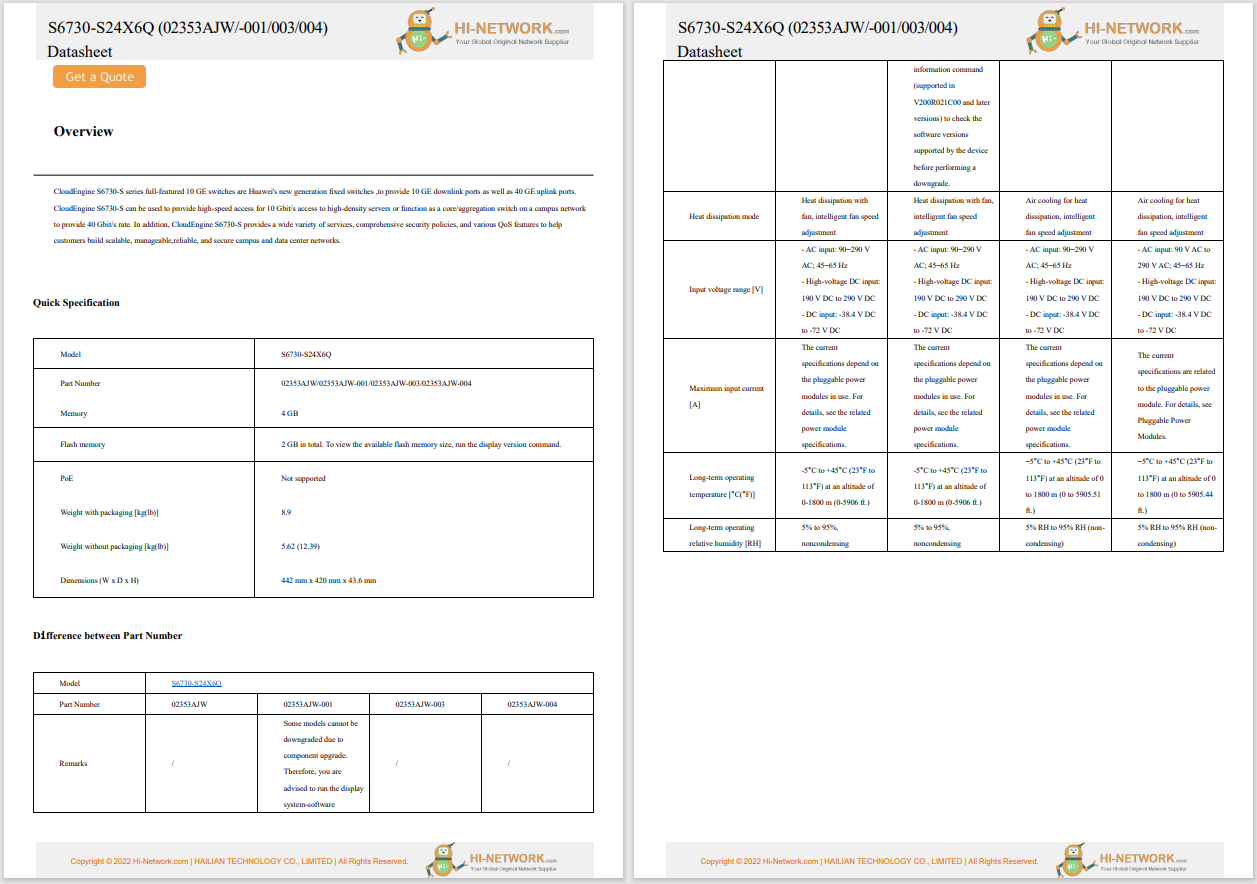













Digital signatures are used to verify the authenticity of a message. For example, when a message is signed, the verifier can rest assured that only the signer could have signed it. ECDSA and DSA are two widely used, standardized digital signature schemes. In order to sign a message, internally both of them require the use of a per-message secret number k that is unpredictable to an attacker. The NIST specifications meet this requirement by generating k randomly and uniformly from a set of integers (modulo q, where q is a sufficiently large prime divisor of the curve order in ECDSA or of p-1 in DSA). It is critical to security that k is unpredictable, since otherwise an attacker could recover the private key. Any two different messages should always be signed with two different and unrelated random k values.
Signature schemes rely on a sound entropy source to generate random values. But in a world in which virtual machines are increasingly utilized, there is the risk that a full snapshot will be restarted more than once which results in a situation in which the entropy state is identical in two or more running instances. This scenario is an abuse of cryptography that should never occur, but in the world of virtualized software, it is a design goal that the guest software not even know that it is running inside a VM. It makes sense, therefore, to think defensively, and look for crypto algorithms whose security isn't degraded by this failure mode. For ECDSA and DSA, this means that it is important to have a process of generating k values that are distinct, even if the initial entropy state is exactly the same. In other words, we need to be certain that two distinct messages will never be signed by the same key k and that they will be signed by uncorrelated random k's. RFC6979 describes such a process. It uses the message itself and the private key value x as inputs to a deterministic random key generation process using a pseudo-random function. This process is deterministic, in that if we sign the same message twice with the same private key, both signatures will use the same k value. This is not a security issue, as it gives no information away; the attack on a reused k value requires two distinct messages to be signed.
NIST's FIPS 186-4 (section 6.3), on the other hand, requires random generation of the key k used in a signature. RFC6979 defines a deterministic process for generating k which does not fall in the acceptable random number generation processes described in FIPS PUB 186-4 Appendix B.5. Until there is a FIPS update or NIST makes an explicit exception, implementations generating k as described in RFC6979 are not officially FIPS compliant.
Like most IT vendors, Cisco certifies the cryptography in many of its products as being FIPS-140 compliant. At the same time, we strive to constantly improve the security of our products, and so we sought ways to address the entropy-fail scenario outlined above within the FIPS framework. To ensure that different messages are signed by different private keys k even if entropy were to fail, we developed this strategy: the signing process introduces message specific pseudorandom information ('additional input' defined in NIST SP 800-90A and SP 800-90C) into the random number generation process used to produce k. Most Cisco products implement this process and thus support FIPS compliant deterministic ECDSA. The process of injecting message-dependent pseudorandom values complies with FIPS 186-4 since k is still generated randomly from the entropy source, and it solves the entropy-fail problem in essentially the same way that deterministic ECDSA/DSA does. Additionally, it avoids the 'double use' of the private key discussed in Section 4 of RFC6979, though admittedly that issue is more theoretical than practical. Of course, we are fans of RFC6979, even though we did not implement it as-is in this case.
 Hot Tags :
fips
digital signatures
Deterministic ECDSA
Hot Tags :
fips
digital signatures
Deterministic ECDSA